Chapter 1: Introduction to Regular Polygons

What is the area of a regular polygon with 100 sides? And how does this apply to any regular shape with 'n' sides?

To calculate the area of various shapes, we start with familiar formulas: the area of a triangle is given by 1/2 * base * height, and for a square, it is the length of a side squared. But what about octagons or shapes with 20 sides? Our goal is to derive a formula that can compute the area of any regular polygon based on the number of its sides.

To achieve this, we need to define what constitutes a regular polygon with 'n' sides. You’re likely already familiar with the concept of regular shapes, so the main variable we need to address is size. We can inscribe our polygon within a circle of radius 'r', like this:

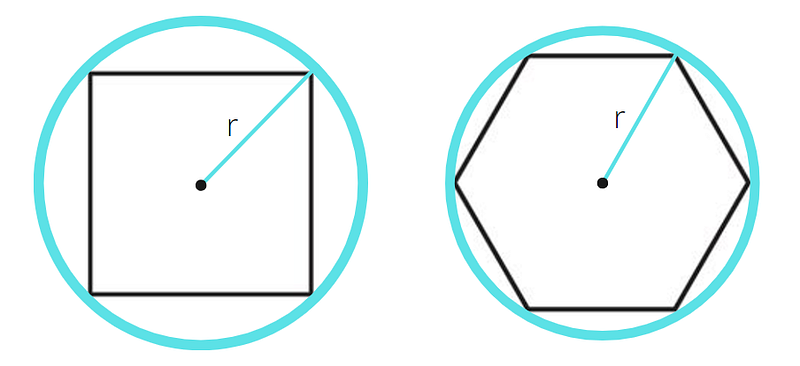
The distance from the center of the polygon to any of its vertices is 'r'.

Chapter 2: Breaking Down the Polygon

To determine the area, we can divide the polygon into triangles. Here’s a visual representation of one of those triangles:

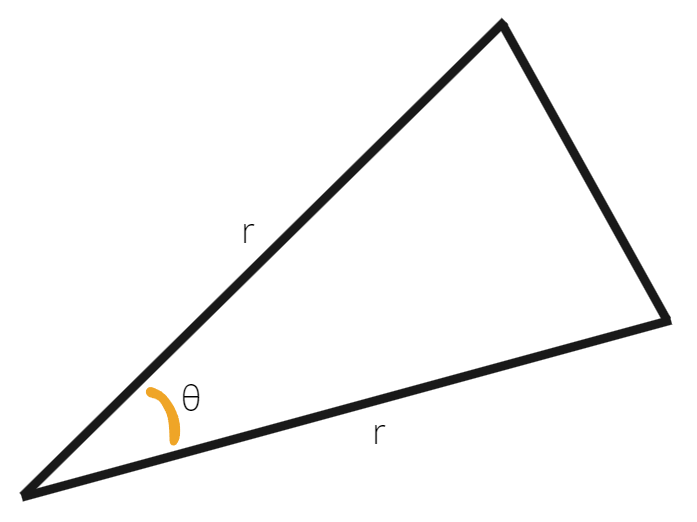
The angle at the apex of this triangle, denoted as θ, is determined entirely by the number of sides 'n'. For now, we will focus on θ and later express it in terms of 'n'.

To find the area of this triangular segment using the information we have, we apply the formula:

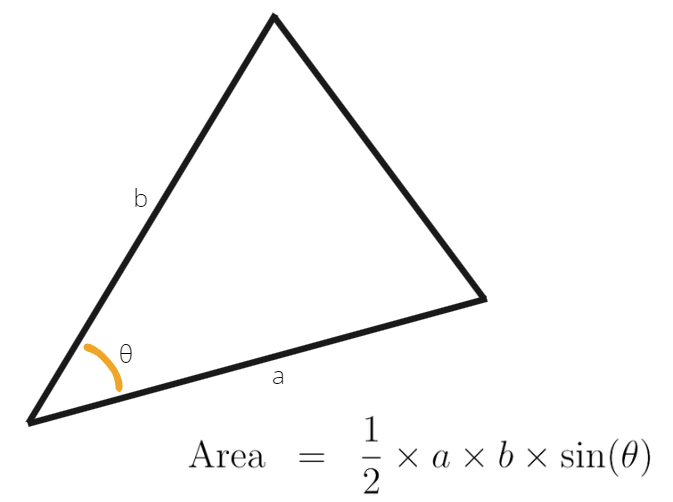
In our triangular segment, both sides 'a' and 'b' are equal to 'r'. Thus, the area becomes:

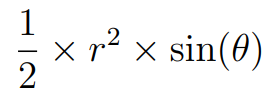
Since a regular n-sided polygon is comprised of 'n' of these triangles, the total area of the polygon is:

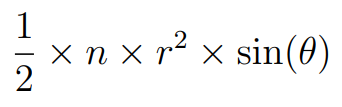
Now, what is θ? The polygon is divided into 'n' equal triangles, so θ equals 360 degrees divided by 'n'. We will use radians instead of degrees for our calculations. Since 360 degrees is equivalent to 2π radians, we have θ = 2π/n.

By substituting this into our earlier area formula, we arrive at:

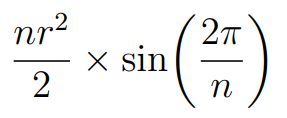
This is our final formula. Remember to set your calculator to radians mode before applying this formula; many students, including myself, have lost marks on tests for forgetting this detail.

Chapter 3: Understanding the Limits

Here are the areas of some regular polygons:

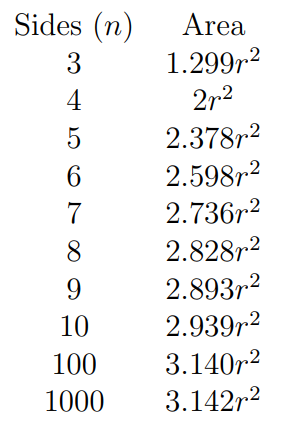
As the number of sides increases, the area approaches πr², which is the area of a circle. This observation becomes increasingly evident as the polygon's sides increase, making it resemble a circle more closely.

Even with a regular polygon boasting a million sides, the difference from a circle becomes negligible.

To challenge yourself, try calculating the area of a regular polygon with 20 sides, assuming each side measures 1 unit. Consider how the area behaves as 'n' increases, particularly under the assumption that all polygons maintain a side length of 1.

This video, titled "Area of a 100 Sided Polygon," goes through the derivation and calculations needed to understand the area of polygons with many sides.

In this video, "How to Calculate the Area of Polygons," you will find practical steps for calculating areas of various polygon types, including regular shapes.