Chapter 1: Introduction to Richard Feynman

Richard Feynman, an iconic American theoretical physicist, is renowned for his groundbreaking work in physics. He was awarded the Nobel Prize in Physics in 1965 alongside Julian Schwinger and Shinichiro Tomonaga. His contributions have made him one of the most respected figures in the scientific community. In a 1999 survey conducted by Physics World, Feynman was recognized as one of the top ten physicists in history.

Feynman's significant contributions include the path integral formulation of quantum mechanics, the development of quantum electrodynamics (which introduced the now-famous Feynman diagrams), and the theoretical foundations of superfluidity in liquid helium. He was also a pioneer in quantum computing and the concept of nanotechnology, among many other achievements.

Feynman once articulated his perspective on the nature of science, stating:

“If you expect science to provide all the answers to profound questions about our existence, you might be disappointed and seek mystical explanations instead. Science is about exploration and understanding the world, not necessarily about uncovering ultimate truths. My pursuit in science is to learn more about nature, and the more I discover, the richer my understanding becomes.” — Richard Feynman

Chapter 2: Feynman's Calculus Journey

In the early 1930s, while attending Far Rockaway High School, Feynman began compiling a set of handwritten notes inspired by a book titled Calculus for the Practical Man. At that time, it was quite rare for high school students to engage with calculus, as many relied on teachers for instruction. This series by J.E. Thompson aimed to equip individuals with practical knowledge of calculus without formal teaching. Feynman thoroughly absorbed the material, reading the book from cover to cover.

As highlighted in Physics Today, “Feynman’s notes exemplify his defining trait: an unquenchable curiosity. When faced with a topic of interest, he was determined to master it independently.”

Section 2.1: Differentiating Functions the Feynman Way

Feynman's approach to differentiation is detailed in the book by Feynman, Leighton, and Sands, which I will refer to as FLR. He presents an efficient method for computing derivatives of complex multi-product functions.

Derivatives of Basic Functions

The foundational derivatives necessary to grasp Feynman's method are as follows:

Derivatives of More Complex Functions

In FLR, a key example is presented, which I will adapt slightly by including a constant in the first term:

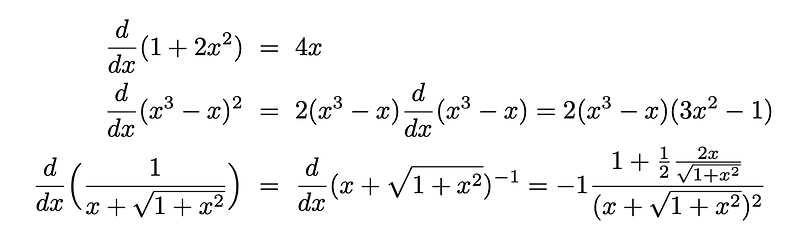
Following Feynman's lead, the initial step involves repeating the two components of f(x), each multiplied by an unknown expression:

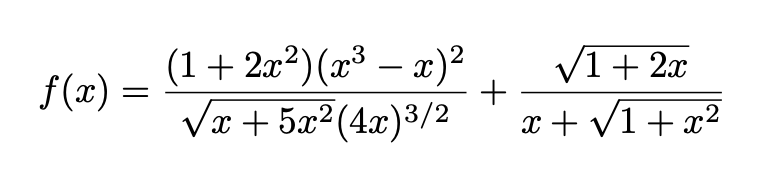
This expression can be simplified as follows:

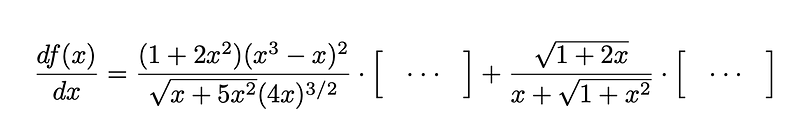
The terms within the brackets will be functions combined through summation. To derive each term, one follows this three-step algorithm. Taking the first factor, (1+2x²), for example, the steps are:

1. This factor becomes the denominator of the first term.
2. The exponent (1) becomes the pre-factor of the first term.
3. The derivative of this factor serves as the numerator of the first term.

The subsequent diagram illustrates this algorithm:

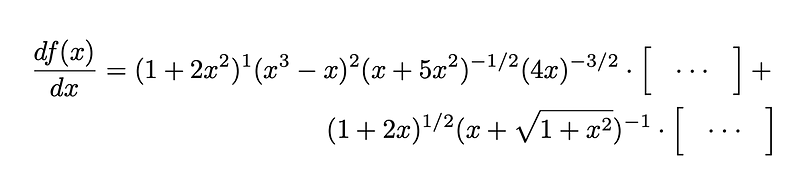
Next, applying the algorithm to the second factor of f(x):

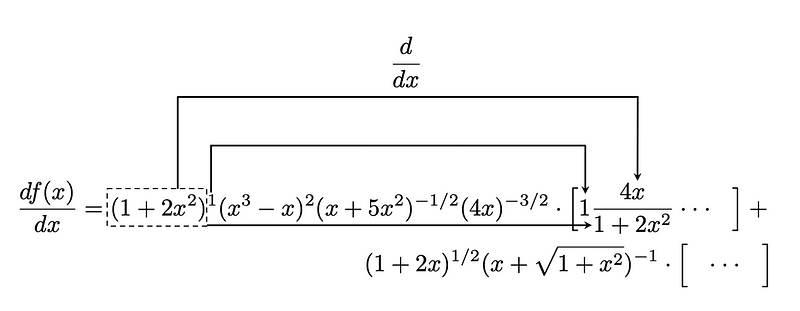
When this process is repeated for all terms, we arrive at the derivative of f(x):

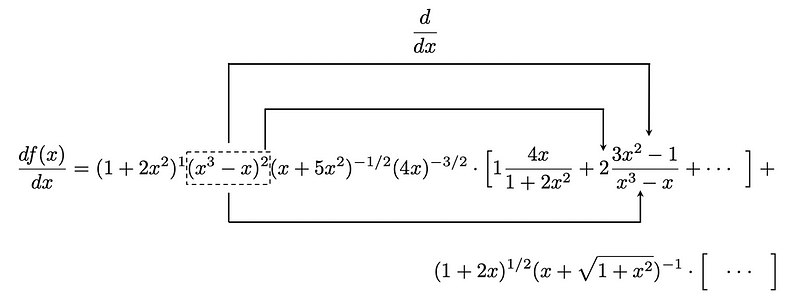
Generalizing the Algorithm

The example in FLR consists of two terms, each fitting the following model:

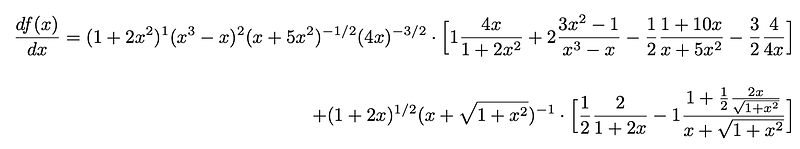
Thus, the generalized form of the derivative can be expressed as:

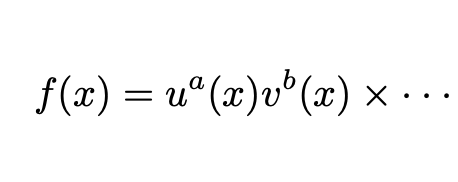
Thanks for reading, and I look forward to your thoughts! For more insightful content on mathematics, science, and beyond, feel free to visit my LinkedIn, personal website at www.marcotavora.me, and GitHub.

This first video, "Feynman's Integral Trick with Math With Bad Drawings," delves into the clever strategies employed by Feynman to tackle mathematical integrals effectively.

The second video, "Feynman's Unique DIFFERENTIATION Technique," explores Feynman's innovative approach to differentiation, illustrating his methods in a captivating manner.