Understanding the Newton-Raphson Method

Among various numerical methods, the Newton-Raphson method stands out for its simplicity and robustness. The initial step in most numerical approaches is to rearrange the equation into the standard form f(x) = 0. For instance, transforming e^x = x into e^x - x = 0.

This leads us to the central question: what are the roots of f(x)?

The Newton-Raphson method estimates roots using tangent lines. The process is illustrated in the following diagram:

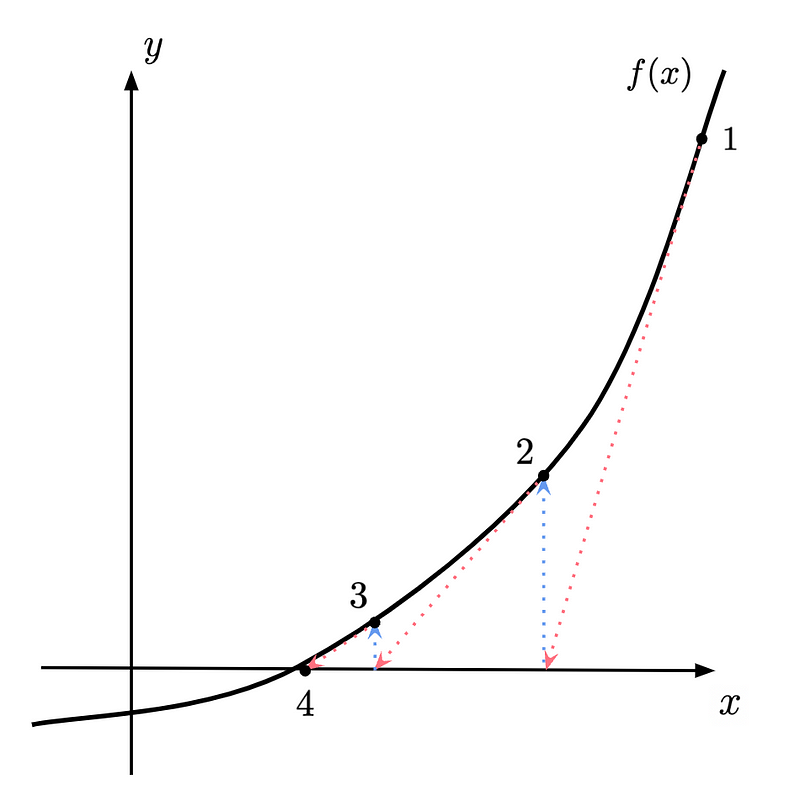
We begin with an initial guess for the root's location and determine the corresponding value on the graph, denoted as point 1. Next, we calculate the tangent line at this point and find where it intersects the x-axis, represented by the red arrow originating from point 1. This intersection provides our updated guess, which ideally brings us closer to the true root. We repeat this process until we reach a satisfactory approximation, as demonstrated by the final point in the diagram.

The Algorithmic Steps

Having grasped the concept of the Newton-Raphson method, let's outline the specific algorithm involved.

1. Initialize an initial guess for the root, denoted as x₀.
2. Transition from the initial guess to a new estimate by adding or subtracting a value (Δx) to/from x₀, yielding x₁ = x₀ + Δx. This Δx serves as a correction to our current estimate.
3. Calculate Δx using tangent lines as described previously. The tangent line at x₀ can be expressed as:

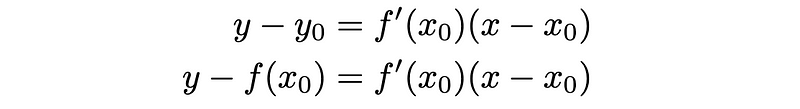
To find the x-intercept of this tangent line, we set y = 0, leading to the following expression for Δx:

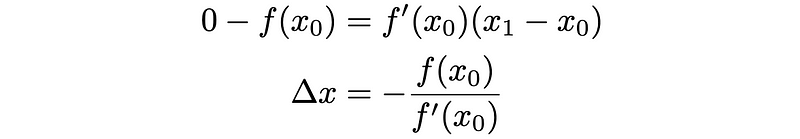
Where Δx = x₀ - x₁.

Thus, for each iteration, we calculate Δx and update our approximation accordingly. The algorithm can be summarized as follows:

1. Start with a reasonable initial guess for the root.
2. Calculate f(x) and f’(x) at the current x-coordinate, and use them to compute Δx.
3. Update the x-coordinate with Δx.
4. If f(x) is sufficiently close to 0, the current x-coordinate is deemed the approximate root; otherwise, repeat steps 2 and 3.

A 'sufficiently close' value could be in the range of -10⁻⁶ to +10⁻⁶, adjustable based on desired accuracy.

Implementing the Method in Python

With the algorithmic steps laid out, we can now implement them in Python code. We will begin by defining the function whose roots we aim to find. For instance, to solve the equation exp(x) = x², we can define f(x) = exp(x) - x² using the following:

def f(x):

return exp(x) - x**2

Next, we also need the derivative, f’(x). This can be done manually, yielding f’(x) = exp(x) - 2x, but we can also calculate this numerically. We will use the forward-difference approximation for the derivative:

def deriv_f(x):

return (f(x + dx) - f(x)) / dx

With both functions defined, we now create the function that implements the Newton-Raphson algorithm:

imax = 100 # Maximum iterations

error = 1e-6 # Acceptable error threshold

def newton_raphson(x_current):

for it in range(imax + 1):

if abs(f(x_current)) < error: # Check if f(x) is close to 0

print(f"Root found, x = {x_current}, in {it} iterations")

break

delta = -f(x_current) / deriv_f(x_current) # Compute Δx

x_current += delta # Update x

if it == imax:

print("Root not found")

Finally, we run the code using an initial guess of x = 0:

dx = 0.1

newton_raphson(0)

Upon execution, the output indicates the approximate root, which in this case is x = -0.7034674784851787, confirmed by verification.