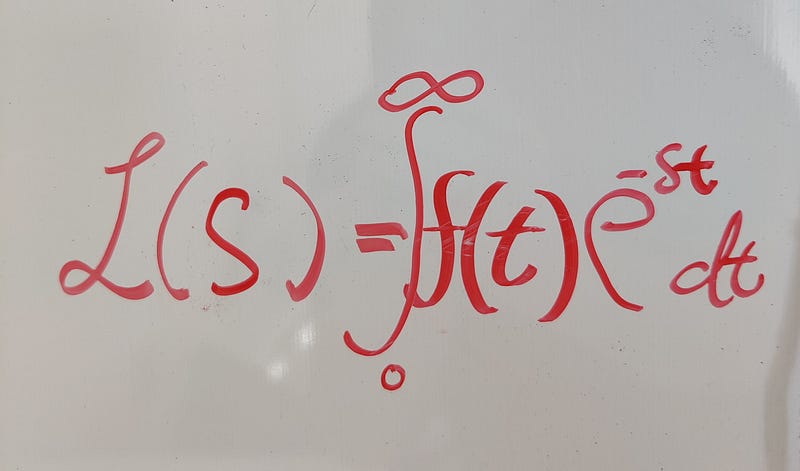Definition and Basic Examples

Before diving deeper, it's essential to clarify what the Laplace transform actually is. While it may initially appear daunting, understanding its fundamental principles and a few examples can greatly demystify it. This article will not delve into convergence issues, as they fall outside its scope. Instead, we will present formulas applicable within their convergence limits.

The Laplace transform is defined as follows: Given a function ( f(t) ), the Laplace transform ( mathcal{L}(f) ) produces another function ( F(s) ):

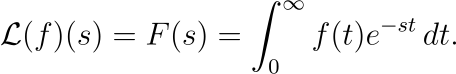
In physical terms, this transformation shifts a signal from the time domain to the complex frequency domain, akin to its relationship with the Fourier transform. Notably, ( F ) is not merely the antiderivative of ( f ), and the integral's upper limit signifies a limit process—assuming it exists.

To illustrate, let's analyze a straightforward function: ( f(t) = t ). Using integration by parts, we find:

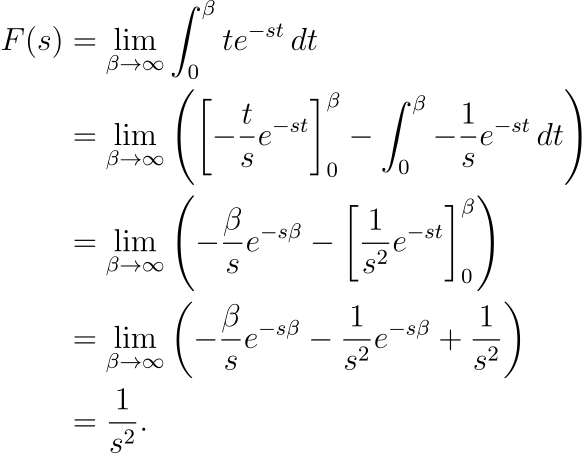
From this example, we see that when ( f(t) = t ), then ( F(s) = frac{1}{s^2} ). A simpler case where ( f(t) = 1 ) results in ( F(s) = frac{1}{s} ).

Exploring the Transform's Properties

As we proceed, we will examine how multiplying by an exponential function modifies the argument in the ( s )-domain, a principle frequently encountered in literature.

This video, "Laplace transforms of power functions," showcases how the Laplace transform can simplify complex functions and their properties.

Next, consider the Laplace transform of the exponential function:

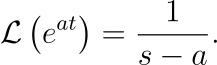
Similarly, we can apply the transform to trigonometric functions. For instance, transforming ( f(t) = sin(t) ) through integration by parts leads us to valuable results:

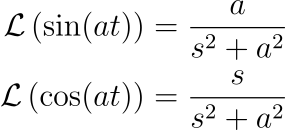
The Laplace transform boasts numerous beneficial properties, including its nature as a linear operator:

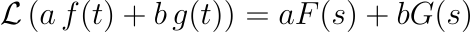
Another pivotal aspect is its one-to-one mapping, ensuring a unique inverse transform exists. This ensures that actions in one domain have corresponding effects in the other.

The Elegance of Euler's Equation via Laplace Transform

One of the most celebrated results in mathematics, known as Euler's formula, demonstrates the relationship between exponential and trigonometric functions:

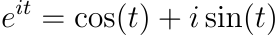
Traditionally, proving this involves expanding the infinite series of the exponential function, which can be technically challenging. However, it can also be verified using Laplace transforms:

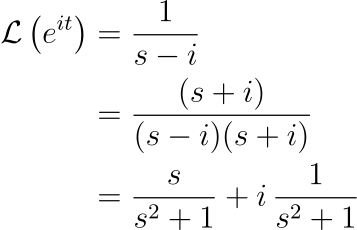
Upon taking the inverse Laplace transform, we arrive at:

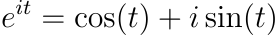
Transforming Derivatives into Polynomials

A remarkable feature of the Laplace transform is its ability to convert derivatives into polynomials. Specifically, multiplying by ( s ) in the ( s )-domain corresponds to differentiating in the time domain:

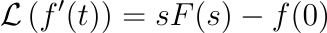
This fundamental property allows for the transformation of differential equations into polynomial equations, significantly simplifying the solving process.

Example: Solving a Differential Equation

Consider the differential equation:

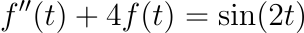
By applying the Laplace transform, we can simplify this equation into:

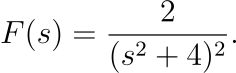
This transformation reduces a complex equation to a straightforward function definition, where initial conditions are seamlessly integrated into the solution.

In the video "Laplace Transform Ultimate Study Guide," viewers can learn more about the practical applications and techniques surrounding Laplace transforms.

Conclusion: The Broader Implications of the Laplace Transform

The ability to manipulate functions through the Laplace transform leads to remarkable applications across various fields, including signal processing and differential equations. The correspondence between multiplication and differentiation, as well as other transformations, highlights the versatility of this mathematical tool.

Ultimately, the Laplace transform has significantly influenced my mathematical journey, serving as a foundational concept that continues to inspire curiosity and understanding.