Understanding Errors and Accuracy in Numerical Computation
Written on
Chapter 1: Introduction to Numerical Errors
When working with floating-point numbers on digital computers, achieving complete accuracy is often unrealistic. Typically, results that are accurate to about ten digits are deemed satisfactory; however, even this level of precision is not always guaranteed. The various types of numerical errors and their impacts on calculations are central themes in numerical analysis, which we will illustrate through several examples.
Example 1: Solving the Quadratic Equation
The quadratic equation
has two precise solutions:
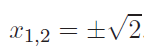
Nevertheless, a digital computer is incapable of computing these solutions in floating-point form exactly. While it can achieve high accuracy (usually up to 16 digits), the true value requires an infinite number of decimal digits, which is beyond the capacity of a computer. Therefore, square roots must be approximated within a specific tolerance, leading to numerical errors.
Example 2: The Sine Function
The sine function is defined as:
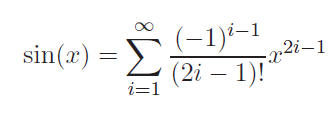
In practical applications, this expression cannot be evaluated with infinite terms. Instead, we must truncate it at a finite value ( n ), which introduces a numerical error, especially for large ( x ). The truncated sum becomes a polynomial of degree ( n ) in ( x ). It is important to note that while the sine function is bounded, no polynomial shares this property. Errors that arise from this truncation are known as truncation errors.
Example 3: The Decimal Representation of 1/10
The fraction ( frac{1}{10} ) is well-defined in decimal form. However, when a digital computer translates it using powers of 2:
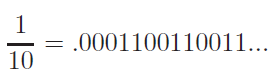
This infinite expansion must be truncated, which means that ( frac{1}{10} ) cannot be represented accurately by a computer. This leads to the unexpected conclusion that multiplying ( 10 times 0.1 ) does not yield the exact value of ( 1.0 ); instead, it misses by approximately ( 10^{-16} ). For additional insights, refer to Section 2.4.
Example 4: Behavior of Functions Near Zero
The function
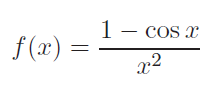
is depicted in Figure 2.1.
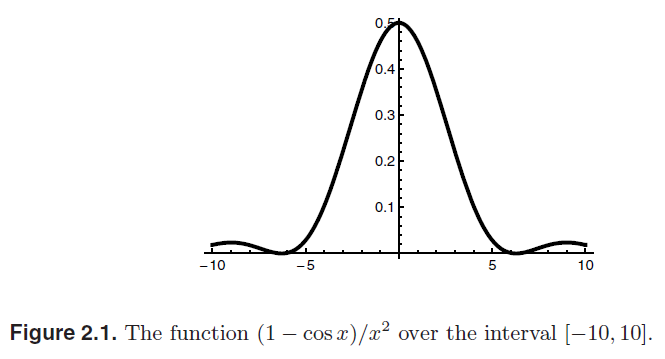
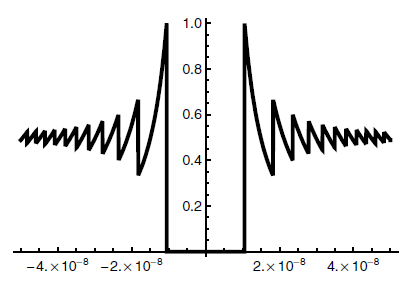
It can be demonstrated that ( f(0) = 0.5 ); near ( x = 0 ), the function behaves similarly to the constant value ( y = 0.5 ). However, when we plot ( f ) over a very narrow interval ([-5.0E-8, 5.0E-8]), the resulting graph appears quite erratic. This discrepancy arises from using floating-point numbers: close to ( x = 0 ), the terms ( 1 ) and ( cos x ) are almost indistinguishable. Their difference yields only a few significant digits, resulting in computations that utilize only two or three relevant digits. This phenomenon is known as cancellation error, which contributes to the erratic appearance of the second graph.
Example 5: Avoiding Equality Checks
Due to the potential for numerical errors, it is advisable to refrain from checking for equality among floating-point numbers. Even when equality is anticipated, it often does not hold precisely. Therefore, instead of using ( x == y ), one should check ( text{abs}(x - y) < epsilon ), where ( epsilon ) represents a small tolerance, such as ( 10^{-10} ).
Several software packages, like Maple or Mathematica, facilitate symbolic computations. In symbolic mode, ( frac{1}{10} ) remains unconverted to an approximate binary; square roots are preserved throughout calculations without being reduced to numerical values. This text will focus primarily on numerical computations, essential for analyzing scientific data.
The first video, "Accuracy, Precision, and Error Types," delves into the distinctions between accuracy and precision in measurements, elaborating on the types of errors encountered in numerical computations.
The second video, "S1E3 - Types of Errors in Measurement, and Accuracy vs. Precision," provides an overview of various measurement errors and how they affect the accuracy and precision of computations.