Chessboard Probability Challenge: Can You Find the Solution?
Written on
Chapter 1: Understanding the Problem
Imagine navigating the edges of an 8×8 chessboard, starting from the lower left corner and making your way to the upper right corner.
At each step, you can either move one square up or one square to the right. Your task is to determine the likelihood that your chosen path will pass through the center of the board.
Before reading further, I encourage you to pause for a moment, grab a pen and paper, and give it a try. When you're ready, continue for the solution!
Solution Approach
To tackle this challenge, we'll adopt a structured methodology.
In the context of uniform probability space, we differentiate between the event space and the sample space. The probability is calculated as the ratio of these two spaces.
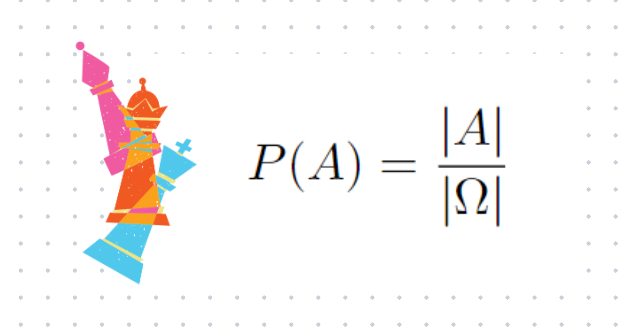
In this scenario, the sample space consists of the various routes one can take to travel from the lower left to the upper right corner, regardless of whether the center is included in the path.
To determine the sample space, we can represent the steps taken as a sequence of letters denoting North (N) and East (E).

One possible route to the destination involves moving north 8 times followed by moving east 8 times.
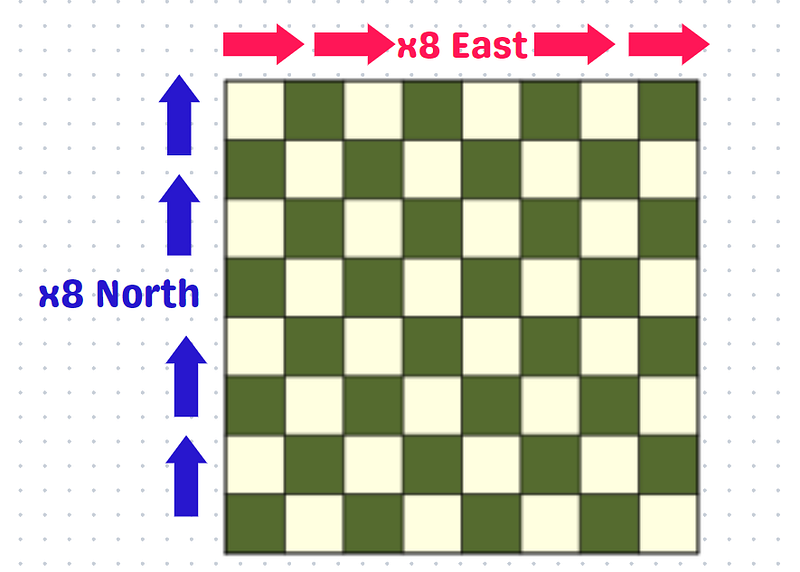
Notably, regardless of the specific movements chosen, the traveler will always move a total of 8 squares up and 8 squares to the right.
Thus, the total number of movement combinations equates to the different ways we can rearrange the letters N and E in our sequence!
Given that we have 16 letters total (8 N's and 8 E's), we need to determine all possible arrangements.
Mathematically, this can be expressed as:
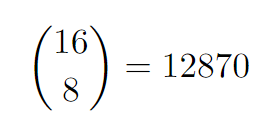
This represents our sample space.
The Event Space
Now, let's explore the event space. To ensure that the traveler passes through the center, we can divide the journey into two segments: the first 8 moves and the final 8 moves.

Our goal is to calculate the number of ways to move from the bottom left corner to the center and then from the center to the upper right corner.
The event space is simply the product of these two segments!
Since both segments form 4 by 4 squares, each sequence will contain 4 N's and 4 E's.
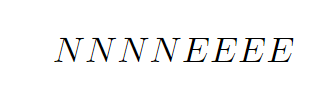
Applying the same reasoning as before, we find that the event space can be represented as:
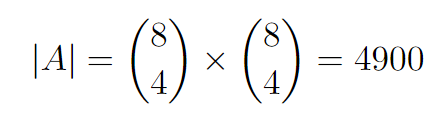
Consequently, the probability is derived from:
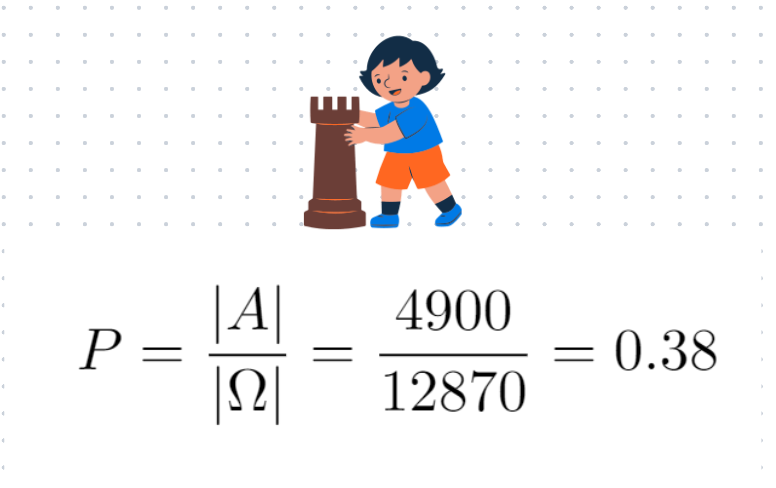
And that concludes our solution!

How incredible is that?
What was your thought process during this challenge? Feel free to share your insights in the comments below; I'm eager to learn!
Math Puzzles
Explore some of the best math puzzles available on Medium, covering various topics such as Algebra, Geometry, and Calculus.
Bella’s Weekly Math Games
Join a thrilling weekly math competition!
This video covers a probability puzzle involving a chessboard and illustrates how to approach similar challenges effectively.
This video showcases an impossible chessboard puzzle that will test your problem-solving skills!
Thank you for taking the time to read this article. If you found it helpful, don't forget to show your support!

If you appreciate my work, consider buying me a coffee as a token of your gratitude. Your support helps sustain my writing and academic journey.
Happy Solving, Bella!