The Breakthrough

By 1843, Hamilton had spent considerable time grappling with the quest to identify numbers in three-dimensional space that would function similarly to complex numbers. While points in three-dimensional space can be expressed as coordinate triples (x, y, z) and easily added together to form vectors, Hamilton struggled to establish a suitable multiplication operation.

In a letter to his son Archibald, he recounted his daily struggle:

"Every morning in early October 1843, you and your brother would ask me, 'Papa, can you multiply triples?' To which I would sorrowfully respond, 'No, I can only add and subtract them.'"

However, on October 16, 1843, while strolling along the Royal Canal in Dublin on his way to a council meeting, Hamilton experienced an epiphany as he crossed Brougham Bridge. He couldn't solve the issue in three dimensions, but he realized he could extend the concept to quadruples (points in four-dimensional space). By employing three numbers from the quadruple as coordinates in three-dimensional space, Hamilton discovered a way to represent points in space that extended into the fourth dimension, allowing the algebra to function correctly. This revelation marked a pivotal moment!

Convinced of the significance of his discovery, Hamilton inscribed the essential multiplication rules onto the stones of the bridge:

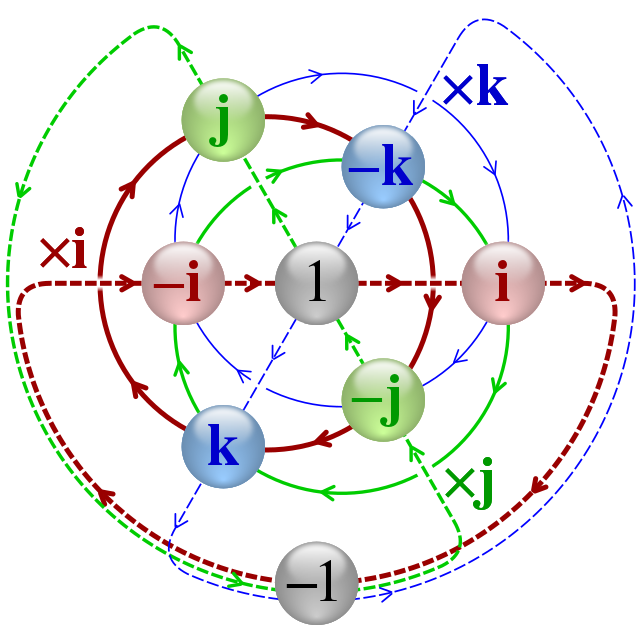
i² = j² = k² = ijk = -1.

His wife likely displayed remarkable patience, waiting in the cold as he celebrated this breakthrough.

The next day, he shared his astonishing experience with fellow mathematician John T. Graves, stating, "And here there dawned on me the notion that we must admit, in some sense, a fourth dimension of space for the purpose of calculating with triples… An electric circuit seemed to close, and a spark flashed forth."

Hamilton termed this new number system a quaternion and dedicated the rest of his life to its study and teaching.

The first video, "Math Encounters -- 'Space, Time, and the Fourth Dimension,'" delves into Hamilton's groundbreaking exploration of higher dimensions and their mathematical implications.

The Mathematics of Quaternions

Similar to complex numbers, quaternions possess both algebraic and geometric aspects. In fact, the field of complex numbers can be viewed as a subset within the quaternion space, suggesting that many properties applicable to complex numbers should also extend to quaternions.

To illustrate, we can organize the number systems as follows:

Natural Numbers → Integers → Rational Numbers → Real Numbers → Complex Numbers → Quaternions.

This leads us to a natural inquiry: Are there number systems with dimensions exceeding quaternions? The answer is affirmative, but before exploring that, let's focus on quaternions themselves.

Quaternions can be represented as points in four-dimensional space, requiring four real numbers for their definition. A quaternion is expressed as q = a + bi + cj + dk, where a, b, c, and d are real numbers, and the symbols i, j, and k adhere to specific algebraic relations:

i² = j² = k² = ijk = -1 (as inscribed by Hamilton).

Importantly, quaternion multiplication is not commutative, meaning qw ≠ wq in general. While this may seem perplexing, those familiar with linear algebra understand that many mathematical structures exhibit this non-commutative property.

We can also express a quaternion as a sum of a scalar part (a) and a vector part (v), written as q = a + v, where v = bi + cj + dk. The conjugate of a quaternion is defined as q* = a - v. The square root of the product of a quaternion and its conjugate yields its norm, representing the distance from the origin in four-dimensional space, illustrating Pythagoras’ theorem extended into four dimensions.

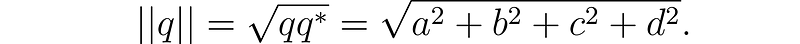
Euler's remarkable relationship connecting the exponential function with trigonometric functions using the complex number i is paralleled by a corresponding formula for quaternions. If q = a + v, a beautiful relationship holds:

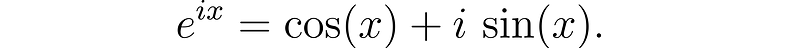
This represents a generalization of Euler’s formula, as evidenced when q = xi (setting a, c, and d to zero), resulting in equivalence between the two formulas.

Hamilton developed these numbers to facilitate rotations in three-dimensional space. Despite existing in four dimensions, quaternions prove effective for managing rotations within three-dimensional frameworks by keeping track of the vector components.

Applications of Quaternions

Quaternions find utility in various mathematical contexts, particularly in the exploration of abstract algebraic structures. Their practical applications are equally noteworthy. For instance, in 3D computer graphics, quaternions are favored for their efficiency, surpassing traditional matrix methods in speed and performance.

They also play a role in one of the proofs for Lagrange’s four-square theorem in number theory, which states that every nonnegative integer can be expressed as the sum of four integer squares. This theorem has implications in areas beyond number theory, including combinatorial design theory and crystallographic texture analysis.

In modern mathematical language, quaternions form a four-dimensional associative normed division algebra over the real numbers and were the first discovered noncommutative division algebra.

As we conclude our exploration of higher-dimensional numbers, it’s essential to note that there are indeed algebras that extend beyond quaternions, referred to as hypercomplex number spaces. The next in this series, the octonions, exist in eight-dimensional space but lack both commutativity and associativity, complicating their application.

I hope this journey through higher dimensions inspires you to delve deeper into these fascinating concepts. For more articles like this one, consider joining Medium for full access. If you're curious about my writing process or daily mathematical insights, feel free to follow me on Instagram:

Kasper Ravnborg Bro Müller (@medium_math) * Instagram photos and videos

Edit description

www.instagram.com

Thank you for your engagement with this exploration of quaternions!