Chapter 1: Understanding Matrices

During your high school years, you likely encountered matrices in your math classes. Like many, you might have found them rather dull and merely tools for calculations. Yet, some matrices possess a captivating group structure, which I aim to explore in this article.

Matrices consist of numbers arranged in either square or rectangular forms. Typically labeled as M, these matrices are defined by their rows and columns, with each element identified by its respective row and column index. For those in computer science, matrices are understood as two-dimensional arrays indexed by two coordinates.

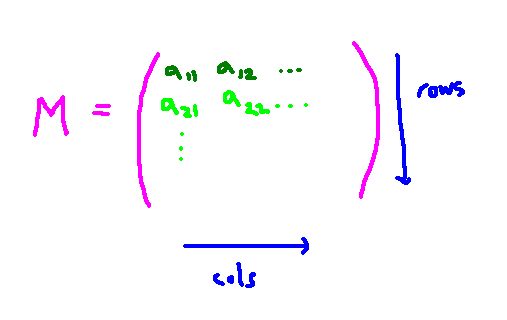
Vectors allow us to denote positions in space, and when a matrix is applied to a vector, it can depict transformations of geometric shapes. Consequently, we can associate matrices with the specific transformations they facilitate. We can categorize matrices based on the characteristics of these transformations. For instance, some matrices may produce well-behaved transformations, while others may not. Certain matrices may scale objects, while others might not.

Section 1.1: Classifying Matrices

As mathematicians, we can group matrices that share similar properties. One interesting aspect is that matrices exhibit distinct "group properties." A primary classification criterion is the type of numbers they contain. For instance, we can have matrices composed entirely of integers or those made up of complex numbers. Thus, we can initially categorize matrices based on the numerical types present within them.

A notable structure from which matrices can be formed is called a field. A field refers to a collection of mathematical entities where addition and multiplication are clearly defined among the elements.

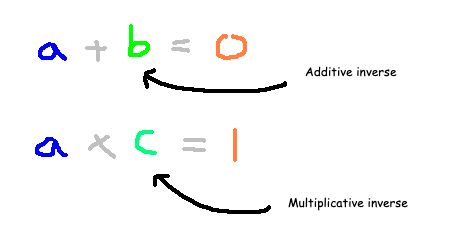
To qualify as a field, certain conditions must be met. Each element in the field should have an additive inverse that returns it to zero upon addition. For example, the additive inverse of 2 is -2 because 2 + (-2) = 0. A similar concept applies to multiplicative inverses, which revert a number to 1 when multiplied. For instance, the multiplicative inverse of 2 is 1/2, satisfying 2 × (1/2) = 1.

It’s crucial to recognize that integers do not form a field. Although every integer has an additive inverse, they lack multiplicative inverses within the set of integers. For any field F, we can establish a set of matrices whose elements are derived solely from that field. The most prevalent fields in mathematics include real numbers, complex numbers, and rational numbers. For a given field F, whether it be C or R, we denote the set of n × n matrices over it as Mat(F).

Section 1.2: The Structure of Matrix Groups

We can create a group from matrices with matrix multiplication serving as the group operation. Like any mathematical group, we require an identity element, inverses, associativity, and closure. An identity matrix exists, and matrix multiplication is associative. However, not all matrices are invertible, preventing this set from being a group by itself. A matrix is invertible only if there exists another matrix that, when multiplied together, yields the identity matrix, which is characterized by ones along the diagonal and zeros elsewhere.

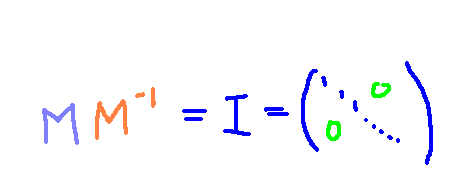
Since many matrices lack invertibility, it is logical to focus on the subgroup of invertible matrices. This collection forms a unique group called the general linear group, GL(n, F), which is recognized as a Lie group due to the smooth nature of matrix multiplication and inversion. We will also demonstrate shortly that GL(n, F) constitutes an open set within Matn(F), establishing it as an n²-dimensional Lie group.

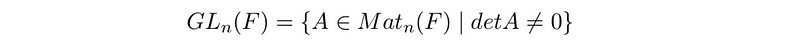
To determine if a matrix is invertible, the determinant must be non-zero. The determinant reflects the volume defined by the vectors composing the matrix. In simpler terms, it indicates how much distortion or scaling the matrix applies to a space, as illustrated in the following diagram.

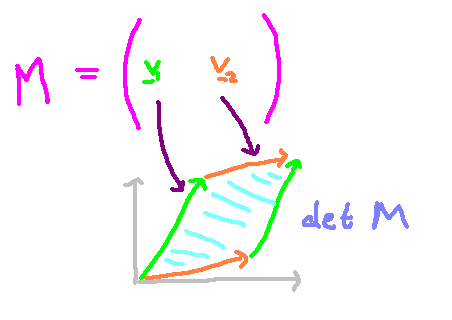
A significant subset of the general linear group is known as the special linear group, SL(F), which includes matrices with a determinant of 1, thus preserving volume. Mathematicians can easily demonstrate that the determinant of the product of two matrices A and B equals the product of their individual determinants. Therefore, if two matrices M1 and M2 have determinants of 1, their product will also have a determinant of 1, indicating that matrices with a determinant of 1 form a group.

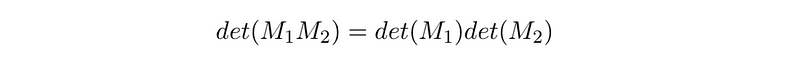
Chapter 2: Dimensions of Matrix Lie Groups

As previously mentioned, matrix groups are considered Lie groups due to their smoothness and manifold structure. This leads us to inquire about the dimension of the special linear Lie group. How many degrees of freedom does it possess? Similar to how a circle is a 1-dimensional Lie group despite being embedded in a 2-dimensional plane, it is mathematically significant to ascertain the dimensions of these matrix groups.

A matrix consists of n² entries, as it comprises n rows and n columns. Therefore, the manifold is a subset of R^(n²). For instance, the special linear group SL(3, R) is a subspace of R³. However, the dimension of SL(3, R) is less than 9 due to constraints placed on the matrices for inclusion in the group.

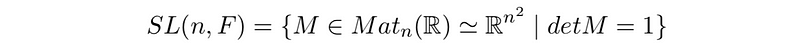
To determine the dimension of this subspace and confirm that the special linear group qualifies as a manifold, we must conduct some tests. The defining criterion for a matrix within the special linear group is that it has a determinant of 1. We can express this condition as F(M), a function that equals zero when the matrix satisfies the criteria.

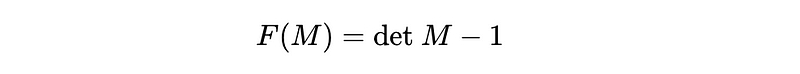
For the SL group to be a manifold, the function M must exhibit a non-zero Jacobian with rank 1. The Jacobian is a measure of how much the function varies as the elements of M change. As a matrix, the Jacobian's rank indicates the number of linearly independent rows it has. Since we have only one condition in the form of F(M), the manifold's dimension is calculated as the dimension of the larger space (n²) minus one due to this additional condition. Thus, the special linear group is an n² - 1-dimensional Lie group.

To compute the Jacobian, we differentiate the function F(M) with respect to each matrix element. We denote the indices i and j to represent the variables being differentiated, which might appear unusual, but we are merely reindexing each component of the matrix in a straightforward manner. The Jacobian element, based on a result we won’t prove here, can be expressed as:

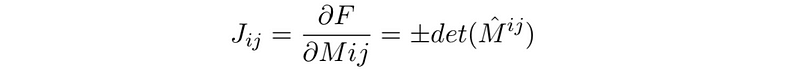
Mˆ ij represents the matrix of minors, which is the (n - 1) × (n - 1) matrix obtained by removing the ith row and jth column. It follows that det(Mˆij) = 0 if and only if det(M) = 0 for all i,j = 1, 2, ..., n. Since our subdeterminants are non-zero, the Jacobian is non-zero and thus has rank one. Consequently, the dimension of our manifold is n² - 1. Moreover, since matrix multiplication and inversion are smooth maps, this confirms it is a Lie group.

This argument can also be extended to complex matrices, where the condition that the determinant equals 1 imposes two constraint functions, as both real and imaginary components are fixed. This approach can be applied to calculate the dimensions of other significant matrix groups, which I have summarized here.

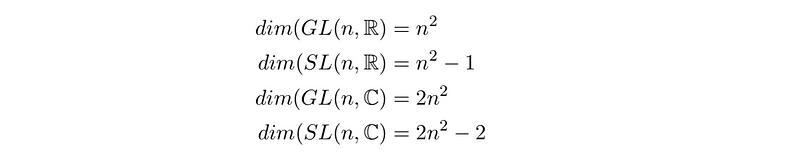
References

In this video, titled "What are Matrix Groups?", we delve into the fascinating structures and properties of matrix groups, providing a comprehensive overview.

The video "Matrix Groups: Part 1" offers an insightful introduction to the concepts surrounding matrix groups, detailing their significance in mathematics.