Understanding Jerry's Atomic Matrix Mass from Rick and Morty
Written on
Chapter 1: The Physics of Floating
Recently, I was persuaded to watch Rick and Morty, and despite its eccentricities, I found it hard to look away. Naturally, this led me to analyze some physics concepts presented in the show, particularly focusing on the character Jerry and his peculiar floating experience in the episode titled Rattlestar Ricklactica.
In this episode, Jerry accidentally falls from his house's roof but is saved by Rick, who uses a ray gun to alter Jerry's atomic matrix. He claims, “I made your atomic matrix SLIGHTLY lighter than air.” This adjustment allows Jerry to float, but then Rick modifies Jerry's shoes, making them “heavier than air,” leading us to question whether Jerry is truly neutrally buoyant. Let’s dive into the physics behind this scenario.
The Buoyancy Force
To understand buoyancy, let's visualize a box of air suspended in the atmosphere, devoid of walls. This box must float; otherwise, all the air would settle to the ground—an odd situation indeed! Assuming this box has a volume ( V ) and the air's density is ( rho_{text{air}} ), we can compute its mass ( m ) and weight ( W ) using the gravitational field ( g ).
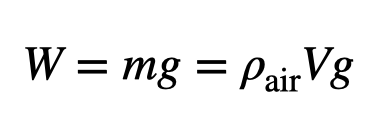
As this box remains suspended, its acceleration is zero, indicating that the net force acting on it must also be zero. Therefore, the buoyancy force must match the weight of the displaced air.
Now, if we substitute the box of air with a wooden box (or any other material), it will experience a similar interaction with the surrounding air, producing an equivalent buoyancy force equal to the weight of the air it displaces. There you have it—the concept of buoyancy!
We can express the magnitude of this buoyancy force using the formula:
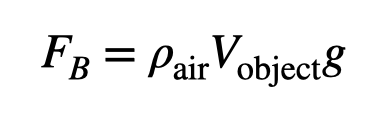
This equation illustrates that the buoyancy force is determined by the air's density (( rho_{text{air}} )), the object's volume (( V_{text{object}} )), and the gravitational field (( g )). Typically, air has a density of approximately 1.2 kg/m³, which means a large wooden block might experience a minimal buoyancy force compared to its actual weight. Hence, normal Jerry does not float; he simply falls from the roof.
Estimating Jerry’s Adjusted Mass
When an object achieves neutral buoyancy, the upward buoyancy force is equivalent to the downward gravitational force, leading to a net force of zero. This principle aligns with Newton’s 2nd Law:
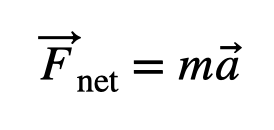
If Jerry is floating, the vertical acceleration is 0 m/s², implying that the net force must equal zero, involving the buoyancy force and weight. Before Rick adds weight to Jerry's shoes, we can estimate the buoyancy force by analyzing video clips from the episode where Jerry jumps after his atomic matrix is modified. Using video analysis tools, I can set a distance scale based on Jerry's assumed normal human size, leading to the following position-time graph.
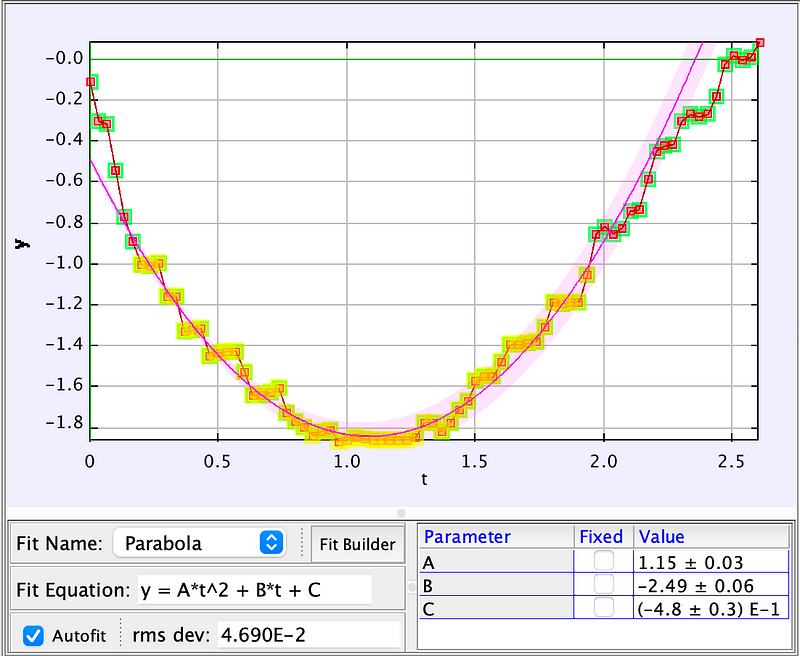
Fitting a parabolic function to this data reveals a calculated upward acceleration of 2.3 m/s². Assuming Jerry's new mass is ( m_2 ), this provides an expression for his adjusted mass.
However, I need to calculate Jerry's volume. Assuming an average adult male weighs 75 kg and has a density similar to water (1000 kg/m³), I can express volume as:
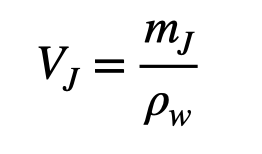
Substituting this into the equation for his new mass (( m_2 )) gives:
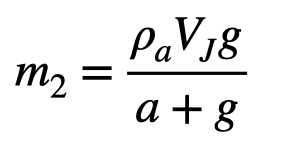
After plugging in values, I arrive at an atomic matrix mass of just 73 grams. However, this calculation lacks consideration for air drag due to his motion, which I’ll omit for simplicity’s sake.
The Mass of Jerry’s Shoes
Rick's adjustment of Jerry's shoes is crucial; if the buoyancy force surpasses the gravitational force, Jerry would float away. Thus, Rick states, “...and now your shoes are heavier than air which makes you neutrally buoyant.” However, this claim is misleading. The weight comparison depends on the amount of air present, and it is clear that Jerry's shoes can't weigh more than the entire atmosphere. What he likely intended to convey is that the shoes possess a higher density than air.
This adjustment allows Jerry to bounce around, as his buoyancy force becomes less than his total weight, despite his reduced mass, which creates a non-negligible force.
Here's a graph illustrating Jerry's vertical position over time with his modified shoes.
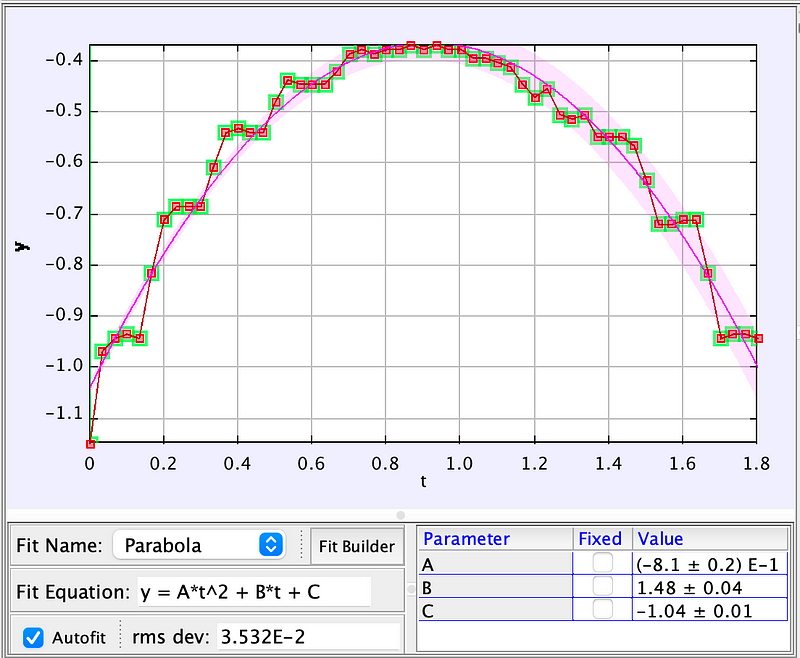
Analyzing this data reveals a vertical acceleration of -1.62 m/s². Knowing Jerry's new mass (( m_2 )), we can establish a force equation.
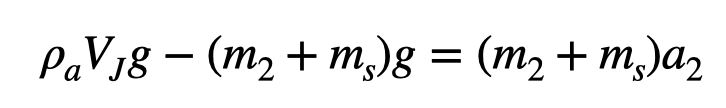
Since we already have Jerry's volume, we can solve for the mass of his shoes (( m_s )):
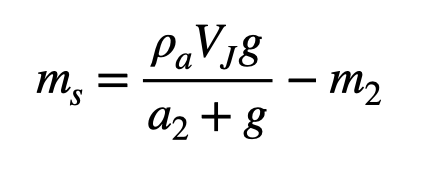
Substituting values gives a total shoe mass of 34 grams for both shoes. To put this into perspective, my own shoes weigh around 600 grams—indicating that Rick's alteration did not make the shoes heavier, but rather reduced their effective density.
Homework Questions
This analysis leaves several intriguing questions unanswered:
- What would happen if Rick hadn't intervened to save Jerry? Estimate Jerry's initial height and impact velocity without considering atomic matrix changes.
- If Jerry's air drag coefficient mimics that of a typical human, does this match his post-ray motion?
- Should Jerry have floated away, what would his terminal upward velocity be in constant density air?
- Assuming Jerry’s effective mass is 76 grams (with altered shoes), how much drag force would act on him at walking speed? What wind speed would be required to lift him?
- At one point, Jerry loses a shoe and starts to float away. What maximum altitude could he reach, considering air density decreases with altitude?
- To bring himself down, how much water would Jerry need to collect in his pants?
- If Jerry weighs 75 grams (missing a shoe) and grabs onto a moving airliner, how much force must he exert with his hands?
Chapter 2: Video Insights
In this video, a biophysicist delves into the scientific elements behind Rick and Morty, explaining how the show's concepts relate to real physics.
Here, a physicist reacts to various moments from Rick and Morty, offering insights into the accuracy and creativity of the show's scientific portrayals.