Chapter 1: Local Perturbations and Time Symmetry

In this section, we aim to demonstrate that slight modifications to the Hamiltonian do not disrupt the underlying time symmetry breaking. To establish this, we need to identify a local unitary operator that connects the altered eigenstates to their original counterparts. Proving that time-symmetry breaking remains intact in the modified scenario hinges on our ability to show that this operator is indeed local. If successful, it implies that we cannot transform long-range correlated states into short-range correlated ones.

Previously, we attempted to develop a local operator, denoted as S, that diagonalizes the perturbed Floquet operator. To confirm its locality, we divided the operator into distinct regions, illustrating that each sub-operator remains confined to its specific area. In the accompanying illustration, V signifies a localized perturbation to the Hamiltonian. This results in a unitary operator S, which evolves our Floquet operators while retaining its local nature.

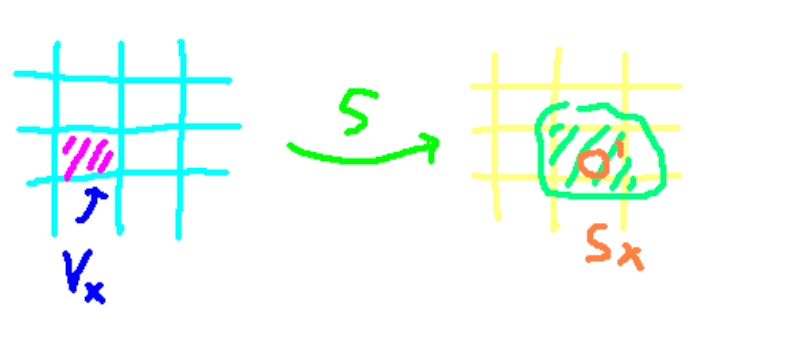
Fourier Expansion and Operator S

The primary objective of this section is to validate that operator S is local. Locality implies that the operator will not transform long-range correlated states into short-range correlated states. If we can prove this assertion, it will indicate that our modified Hamiltonian continues to exhibit time translation symmetry. Consequently, we can express operator S in terms of its matrix elements.

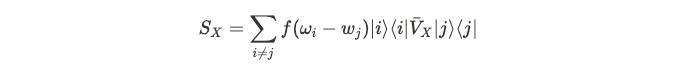
Assuming our Hamiltonian possesses an eigenstate with eigenvalue λ, this suggests that an energy value of λ is detectable in our quantum framework. By exponentiating the Hamiltonian, we derive the time evolution operator, commonly referred to as the Floquet operator when the Hamiltonian is periodic. This time evolution operator shares the same eigenstates. From this operator, we can also determine induced eigenvalues, which are complex numbers with unit modulus. Below, U_H denotes the Floquet operator associated with the Hamiltonian. The eigenvalue of the Floquet operator, termed the quasi-energy eigenvalue, is derived from the original eigenvalue of the Hamiltonian’s eigenstate. We can expand this in terms of the unperturbed Floquet operators, as follows:

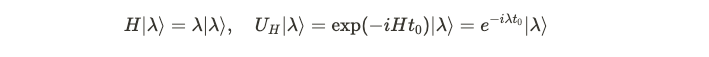
To establish the locality of this operator, we need to demonstrate that these Floquet operators do not extend the support of operator V_X beyond a constant limit. The subscript 0 indicates that the Hamiltonian remains unperturbed. To verify the validity of this expansion, we can contract the state with two eigenstates labeled i and j, allowing us to analyze the results.

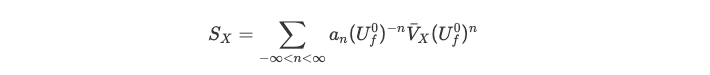
Through this approach, we can confirm that it aligns with the original operator discussed earlier. By applying the unperturbed operator multiple times to the eigenstates, we derive eigenvalues raised to the power of n in the summation, resembling a Fourier series.

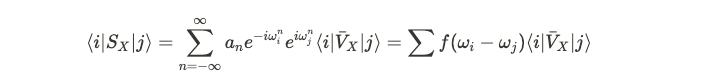
To ascertain that the unperturbed Floquet operator does not excessively increase the support, let’s examine the effects of placing the unperturbed operator adjacent to itself and duplicating it several times. In the most straightforward scenario, we can observe the outcome when we apply the operator twice.

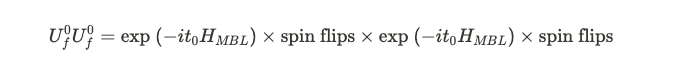
We can consolidate the spin flips to one side, albeit at the cost of altering some signs in the MBL Hamiltonian. This is due to the fact that the MBL Hamiltonian is composed solely of Pauli sigma matrices, ensuring that the support of V_X remains unchanged by more than a constant factor.

Support of Quantum Operators

When we possess an operator and know its eigenstates, we can express it in terms of its eigenstates and eigenvalues.

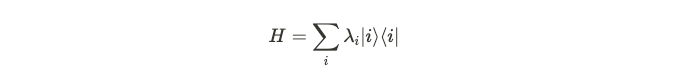
Subsequently, we can deconstruct it into a Fourier series, demonstrating that the coefficients in these series indicate the operator's locality. Specifically, we leverage the fact that applying the unperturbed Hamiltonian n times on operators does not expand the region where the operator is non-zero by more than a constant amount.

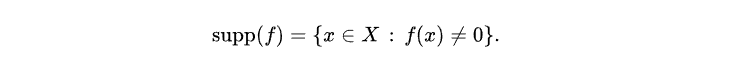
In the context of quantum mechanics, the support of a function refers to the area in the domain where the function is non-zero. How does this concept translate into quantum theory? Quantum states are represented as vectors within a Hilbert space, while quantum operators serve as linear transformations on this vector space. Hence, defining the kernel of an operator entails identifying the set of vectors that yield zero upon application, with the support being the orthogonal complement of the kernel.

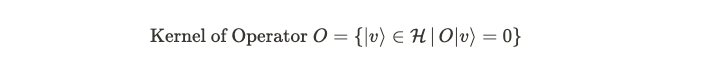
Now that we've delineated the kernel, we can ascertain the support. The orthogonal complement of a subspace consists of all vectors that produce zero when contracted.

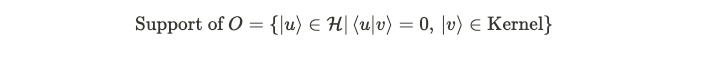
Chapter 2: Exploring Time Crystals

This video titled "Time Crystals: Past, Present, and Future" delves into the history and future implications of time crystals, explaining their unique properties and relevance in modern physics.

In "What is a time crystal? —Norman Yao," the concept of time crystals is unpacked, providing a clear understanding of their principles and significance in quantum mechanics.