Can You Solve This Intriguing Viral Geometry Challenge?
Written on
Chapter 1: Introduction to the Puzzle
Recently, I stumbled upon a captivating geometry puzzle circulating online, and I couldn't resist the challenge. Tracing back to its origins proved to be quite a task, as is typical with viral content. My first encounter with it was through Presh Twalwalkar, who credits an individual named Reio from Romania.
At the heart of this puzzle lies a square featuring a seemingly random point within. This point connects to the midpoints of the square's sides through line segments, thereby dividing the square into four unequal regions. Specifically, the area in the top-left measures 10 cm², the top-right 16 cm², and the bottom-left 8 cm². Your task is to determine the area of the bottom-right section. Are you ready to give it a shot?
Spoiler Alert: If you wish to attempt solving the puzzle independently, I recommend pausing here. Once you've tried, feel free to return for the solution.
Chapter 2: The Solution Approach
To tackle this challenge, we start with the familiar formula for calculating the area of a triangle based on its base and height:
Area of a triangle = ½ * (Base) * (Height)
This formula can be extended to claim that triangles with various shapes but the same base and height will have equal areas.
Consider the illustration below, showcasing three differently shaped triangles that share the same base and height, thus yielding identical areas.
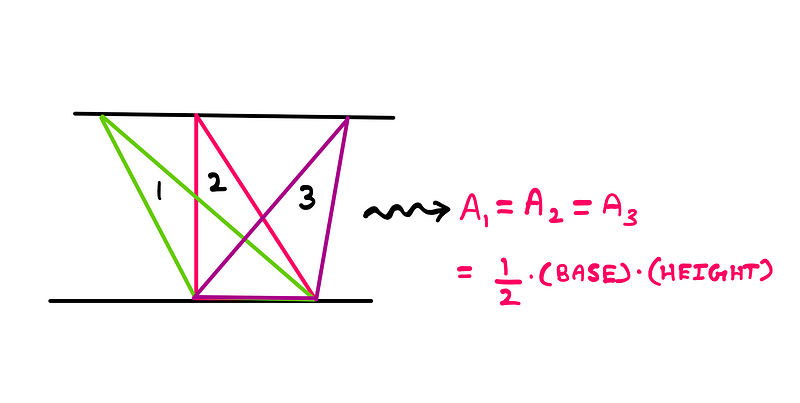
With this foundational understanding, we can now delve into solving the puzzle.
Section 2.1: Creating Triangles Within the Square
While the puzzle presents us with triangles, we need to connect the internal point to the corners of the square to create triangles. This results in eight triangular regions within the square, as illustrated below:
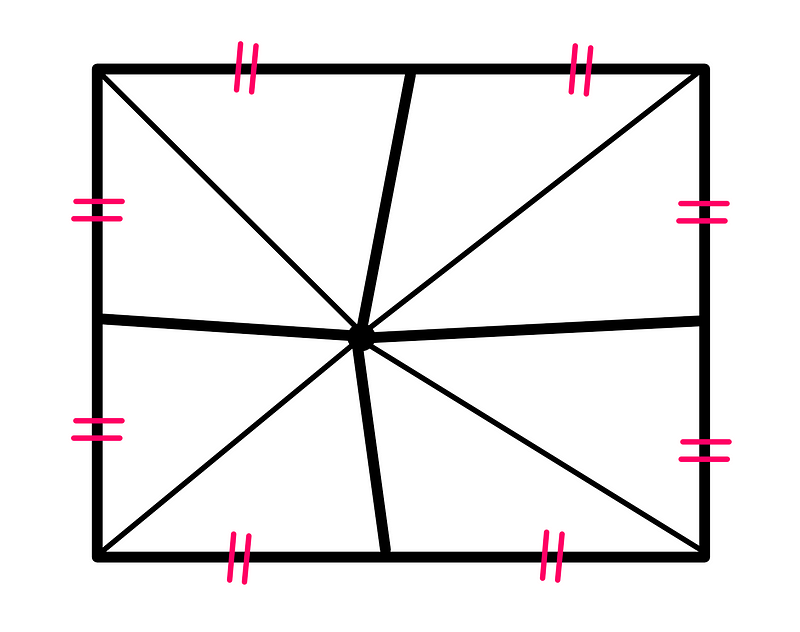
Focusing on the two blue-shaded triangles at the bottom of the square, they share both a base (the bottom side of the square) and height (determined by the internal point).
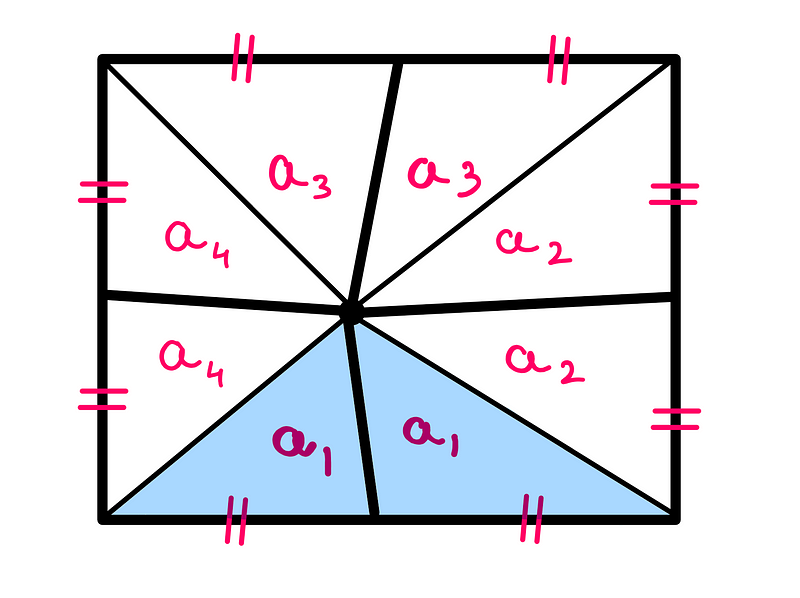
By our earlier insight, these triangles have equal areas, marked as 'a1' for both. Likewise, we can identify three additional pairs of triangles with equal areas ('a2', 'a3', and 'a4').
Section 2.2: Calculating Areas Across Diagonals
Now that we've designated areas for each triangle, we can sum the areas along the left diagonal of the square, from the bottom to the top:
Sum of areas along the left diagonal = (a1 + a4) + (a2 + a3)
Next, we analyze the areas along the right diagonal:
Sum of areas along the right diagonal = (a1 + a2) + (a3 + a4)
Interestingly, the sums of the areas along opposite diagonals are equal:
Sum of areas along the left diagonal = Sum of areas along the right diagonal
? (a1 + a4) + (a2 + a3) = (a1 + a2) + (a3 + a4) ? A
Let's keep this equation (A) in mind. From the puzzle's data, we know:
a1 + a4 = 8 cm²
a3 + a4 = 10 cm²
a2 + a3 = 16 cm²
a1 + a2 = ??
By substituting these values into equation A, we can deduce:
(8 + 16) cm² = (a1 + a2) + 10 cm²
Subtracting 10 cm² from both sides yields:
a1 + a2 = 14 cm²
Thus, the area of the bottom-right section of the square is 14 cm², and the total area of the square is 48 cm².
We initiated this process with the understanding that triangles sharing the same base and height have equal areas. This insight led us to conclude that the sums of the areas along opposite diagonals are equal, enabling us to solve for the unknown area.
Chapter 3: Further Exploration
For those interested in exploring more mathematical concepts, consider checking out "How To Really Benefit From Curves Of Constant Width?" and "What Really Happens When You Divide By Zero?".
If you'd like to support my work, please consider contributing on Patreon.
Explore a viral geometry puzzle solvable through algebraic methods.
Challenge yourself with this viral math puzzle and see if you can find the solution.