Inside a Mathematical Singularity

The fourth dimension of AdS space, characterized by a Klein bottle topology, possesses a time-like attribute. For the sake of argument, let's represent this time-like quality through numbers in the Fibonacci sequence, where each number is the sum of the preceding two, starting with 0 and 1. The values in this sequence continuously grow, eventually reaching a magnitude that leads to a mathematical singularity, bearing similarities to a black hole within AdS space-time when infused with quantum particles and matter.

Tim Andersen noted:

As a mathematician, I am all too familiar with singularities as a calculational convenience to believe they are physical phenomena. Rather, they signify a boundary and indicate a transition from one regime to another.

This perspective aligns with other discussions in this series, suggesting that a mathematical singularity indicates a transition point.

According to cosmologists studying the attributes of AdS space with black holes—also considered mathematical singularities—the interior of a black hole is thought to possess an additional time-like dimension. A black hole within a four-dimensional AdS space comprises three spatial dimensions and two time-like dimensions. Some theorists propose that a black hole may ultimately collapse, with its contents re-emerging in the original AdS space-time, potentially appearing "before" the black hole that originated them. Contrarily, a white hole represents the opposite phenomenon: nothing can enter a white hole. The interplay between black and white holes suggests that the content emerging from a white hole could be akin to a hologram within the boundary of a black hole, as this content would only have one time-like dimension instead of two.

To visualize the relationship between black holes and white holes, see the diagram below:

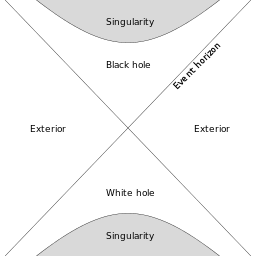
An AdS space-time built from Platonic solids does not yet incorporate energy or particles. However, the Platonic solids within this AdS space continuously expand, creating a mathematical singularity equivalent. These solids grow larger as they embody information about the history of solids entering and exiting Klein bottles (as discussed in the next article in this series). This mathematical singularity is integrated into a boundary in the AdS space-time. The AdS space inside this boundary remains AdS space, possessing its own boundary where two time-like dimensions exist.

As the constituents of AdS space inside a mathematical singularity retain information about the topology of that space, the content within the boundary could be renormalized as if it were another Klein bottle composed of parts exhibiting Klein bottle properties. In short, a mathematical singularity arising in an AdS space-time formed from Platonic solids appears analogous to the black hole/white hole cycle that some contemporary cosmologists propose for AdS space filled with energy and particles. Enormous Platonic solids (Klein bottles) are re-scaled, emerging through what can be considered a "white hole" in the original AdS space-time as smaller solids.

An example of a secondary time dimension that is distinct yet related to the original time-like dimension is the Golden Ratio (φ), defined as the ratio of the sum of two adjacent Fibonacci numbers to the larger of the two. This ratio, an irrational number, possesses infinite decimal expansion with no recurring sequence and cannot be expressed as a fraction of two integers. Since the digits of φ (approximately 1.618033…) never repeat, this sequence exhibits time-like characteristics; a number "later" in the series can only be identified once all preceding numbers have been computed.

Crossing Boundaries

AdS space-time contains boundaries, and nested within these boundaries are additional boundaries. Content enclosed within these boundaries can be described mathematically. According to Spencer-Brown's mathematical framework, crossing an event horizon in AdS space creates a Distinction. Transitioning into a boundary within the AdS space-time also establishes a Distinction. When the mathematics of AdS space-time is delineated by two categories—'inside' or 'outside'—entering a different region necessitates that the status of the second region differs from that of the first. For example, if the first region is 'inside,' the second should be 'outside.' However, when a boundary collapses and its content re-emerges into the original AdS space-time, what becomes of the 'inside' versus 'outside' distinction?

Spencer-Brown's Law of Condensation posits that multiple Distinctions of the same kind, such as crossing over the event horizon of a boundary, condense into a singular Distinction. Conversely, his Law of Cancellation suggests that nested Distinctions can negate one another.

These two laws (Condensation and Cancellation) govern all binary worlds. Existence begins with the establishment of Distinctions by creating boundaries. These laws are the only possible constructs within a space formed by making Distinctions. Regardless of the number of Distinctions made, they ultimately condense into combinations of paired or nested Distinctions. Spencer-Brown's Laws articulate fundamental insights about the archetypal essence of reality, framing our understanding of something and nothing.

In subsequent discussions, Spencer-Brown concludes that space emerges from the mere act of creating a Distinction. Neurobiologist Francisco Varela later argued that incorporating self-referencing into the analysis leads to the emergence of time. Moreover, the cycle of content entering and exiting mathematical singularities may elucidate the genesis of quantum phenomena.

Mathematically, Platonic solids and their duals share identical descriptions when combined with (0, 1) bits of information. The description of a Platonic solid within a boundary can be differentiated from that outside by being its dual. Additionally, a solid within the boundary of a mathematical singularity can be the dual of the solid in AdS space, with the values of the (0, 1) bits of information oscillating between 0 and 1.

Mathematical Singularity and Content in AdS Space-Time

In summary, a three-dimensional AdS space composed of Platonic solids automatically adopts the topology of a Klein bottle. The restructured AdS space acquires an additional time-like dimension, evolving into a four-dimensional AdS space that takes on the topology of a Klein bottle made up of individual Klein bottles. The reintegration of Klein bottles into this macro topology causes the content in AdS space to possess bits of information fluctuating between 0 and 1.

The forthcoming article will elaborate on how an AdS space-time featuring quantum-like attributes gives rise to new phenomena, such as energy and matter. The mathematical framework for this new AdS space-time serves as a foundation for understanding how both consciousness and our universe may emerge.

These articles do not aim to prove the origins of our universe but rather suggest that logical explanations are plausible, countering the notion that our universe is inexplicable.

The focus here is on leveraging the findings of existing research. Once the idea of a logical explanation for our universe gains traction, new investigations may reveal additional concepts that elucidate possible mechanisms in greater detail.

The primary question addressed in this article is:

Could the origin of our universe stem from geometry?

The video titled "Why Space Itself May Be Quantum in Nature - with Jim Baggott" explores the intriguing concept of space potentially embodying quantum characteristics, shedding light on the implications of such a viewpoint.